En 1883 empezó a venderse en Francia un antiguo rompecabezas oriental, rescatado para Occidente por el profesor N. Claus (de Siam) y cuyas primeras referencias eran los escritos del ilustre mandarín Fer-Fer-Tam-Tam. Según una leyenda india, en el Templo de Benarés, bajo el domo que marca el centro del mundo, hay una placa de latón con tres agujas de diamante. Durante la creación, Dios puso sesenta y cuatro discos de oro puro de distinto tamaño en una de las agujas, formando una torre. Los bramanes llevan generaciones cambiando de lugar, uno a uno, los discos de la torre entre las tres agujas de forma que en ningún momento un disco mayor descanse sobre otro más pequeño. Cuando hayan conseguido trasladar todos los discos a otra aguja su trabajo estará terminado, y la torre y el templo se derrumbarán, y con un gran trueno, el mundo se desvanecerá. La versión simplificada que se vendía en Francia se componía de ocho discos de madera.
En realidad, la Torre de Hanoi y la leyenda india habían sido inventadas por el matemático francés Édouard Lucas (N. Claus de Siam es un anagrama de Lucas d'Amiens). Su compatriota, el escritor Henri de Parville amplió y adornó la leyenda poco tiempo después. A pesar de que el reto planteado es relativamente sencillo, la idea de Lucas ha demostrado ser una de las más fecundas de la historia de las matemáticas recreativas.
Si no lo has hecho antes, antes de seguir leyendo tal vez deberías familiarizarte con el rompezabezas y resolverlo por ti mismo. Puedes usar un modelo real o uno de los muchos simuladores que hay disponibles en Internet (mira en los enlaces del final).
Los discos se numerarán de 1 a 8 (o a n, en general), empezando por el más pequeño. Los postes (que se supondrán alineados de izquierda a derecha) serán marcados con letras mayúsculas (A, B y C). El inicial será A y el objetivo C.

fig. 1
La Torre de Hanoi suele aparecer como ejemplo para ilustrar el concepto de recursión en los cursos de programación de computadoras, ya que existe un algoritmo recursivo sorprendentemente simple que lo resuelve (por si alguien no lo sabe, un algoritmo es recursivo si se llama a sí mismo en alguno de sus pasos). Supongamos que queremos trasladar los ocho discos del poste A al poste C. Como el disco 8 siempre está abajo del todo, la única forma de hacerlo es trasladar primero la torre de siete discos 1...7 al poste B. Entonces podremos llevar el disco 8 de A a C, y para terminar tendremos que trasladar de nuevo la torre 1...7, ahora de B a C.

fig. 2
Pero los discos 1...7 forman una torre totalmente similar a la inicial, así que en dos de los tres pasos anteriores nos enfrentamos con un problema análogo al original. De hecho, puede resolverse de la misma forma, trasladando ahora la torre 1...6. Por ejemplo, el primer paso (trasladar la torre 1...7 de A a B) se puede descomponer en estos tres pasos.

fig. 3
Por supuesto, en dos de estos tres pasos nos volvemos a encontrar con el problema original, ahora con n = 6. El proceso no es infinito, ya que llega el momento en que trasladar una torre equivale a trasladar un solo disco (esto ocurre cuando la torre es de un solo disco, claro). En resumen, el algoritmo recursivo es el siguiente.
Algoritmo para trasladar la torre 1...n del poste X al poste Z, usando como auxiliar el poste Y.
Este algoritmo siempre me ha parecido sorprendente, parece más la definición de un problema que su resolución. Si eres como yo tendrás que implementarlo en un lenguaje de programación concreto para convencerte de que funciona. En realidad, lo único que hace es especificar unos pasos inevitables. Por ejemplo, como vimos antes, para resolver el puzzle es obligatorio llevar el disco n de A a C, y para ello es obligatorio llevar antes la torre 1...n a B, etc. La secuencia de movimientos que produce este algoritmo es la única solución óptima (o sea, de longitud mínima) posible. El número de movimientos es M3(n) = 2n−1, como se puede demostrar fácilmente por inducción sobre el número de discos.
Se cumple para n = 1
M3(1) = 1 = 21−1.
Si se cumple para n, se cumple para d+1
Al ejecutarse el algoritmo para n+1 se llama a sí mismo dos veces
para n, más un movimiento del disco n+1. Así que
M3(n+1) = 2 × M3(n) + 1 = 2 ×
(2n−1) + 1 = 2n+1−2+1 =
2n+1−1.
Para n = 8 el número de movimientos es de 28−1 = 255. Para n = 64, de 264−1 = 18.446.744.073.709.551.615. Si los bramanes de Benarés cambiaran un disco de sitio cada segundo necesitarían más de quinientos ochenta mil millones de años para terminar su tarea, unas cuarenta veces la edad del Universo.
Los algoritmos recursivos funcionan bien con ordenadores, pero son difíciles de aplicar para un ser humano. Si intentas resolver la torre de ocho discos aplicando el método descrito es fácil que te pierdas a no ser que vayas tomando notas de por dónde vas. Incluso para los ordenadores los algoritmos recursivos suelen ser «poco económicos», en el sentido de que consumen bastante memoria (y es que ellos también necesitan «tomar notas»). La alternativa a los algoritmos recursivos son los iterativos, en los que no hay llamadas a sí mismo, sino uno o varios bucles. Muy a menudo no existe o no se conoce una alternativa iterativa para un algoritmo recursivo, y cuando sí se conoce, suele ser mucho más complicada que la versión recursiva. Sin embargo, en el caso de la Torre de Hanoi, existen varios algoritmos iterativos muy simples.
Antes de buscar un algoritmo iterativo resaltemos de nuevo un detalle importante. Aunque estamos hablando de varios algoritmos, la solución óptima (la de menos movimientos, que como hemos visto antes, para n = 8 es de 255) es única. O sea, la serie de movimientos que resulta de aplicar un algoritmo (óptimo) cualquiera será siempre la misma.
Una observación clave para encontrar un algoritmo iterativo es que el disco más pequeño se mueve una vez sí, una vez no. El primer movimiento hay que hacerlo con el disco 1. Está claro que después de mover el disco 1 (en cualquier ocasión) se debe mover un disco distinto (si no queremos perder el tiempo moviendo el mismo disco varias veces). Este movimiento debe hacerse entre los dos postes que no contienen el disco 1. A continuación no nos quedan más que dos alternativas: deshacer el último movimiento, lo que no tiene sentido, o volver a mover el disco 1. Además, cuando le toque le toque el turno a un disco distinto de 1, el movimiento estará perfectamente determinado ya que sólo intervendrán dos postes, y entre dos postes sólo hay un movimiento posible. Así que sólo puede haber duda cuando hay que mover el disco menor. Se sale de esta duda respetando una cualquiera de las siguientes reglas.
Teniendo en cuenta la primera regla se construye un algoritmo descubierto por Peter Buneman y Leon Levy.
Teniendo en cuenta la segunda regla, el algoritmo podría ser el siguiente.
Para hacer este algoritmo más fácil de aplicar se pueden pintar los discos pares e impares de dos colores distintos. Incluso se puede pintar la base en tres trozos, como se ve en el dibujo (es como si los trozos de base fueran los discos n+1, n+2 y n+3).

fig. 4
Con esta versión del rompecabezas el último algoritmo se puede redactar así:
El disco más pequeño no es el único que no se coloca nunca sobre otro de distinto color, en ningún momento hay dos discos del mismo color juntos.
Analizando otra vez el algoritmo recursivo y el razonamiento que nos llevó a él podemos comprobar que (centrándonos en el caso de 8 discos) el disco 8 se mueve una sola vez, el 7 dos veces, el 6 cuatro veces, etc. El disco 1 se mueve 128 veces. La suma de estas potencias de 2 coincide con el total de movimientos antes calculado (1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255). En general, el disco k se mueve 2n−k veces, y 20 + 21 + ... + 2n−1 = 2n−1.
Vamos ahora a fijarnos en los momentos concretos en que se mueve cada disco. Para empezar trataremos el caso de cinco discos que en esta ocasión pintaremos con cinco tonos de azul.

fig. 5
Ilustraremos los movimientos mediante una tira de 31 cuadrados, cada uno de los cuales representa un movimiento de la solución. Iremos coloreando estos cuadrados progresivamente con los colores de los discos, empezando por el disco mayor y yendo hacia arriba en la torre.

fig. 6
El disco mayor (el 5 en este caso) protagoniza el movimiento central, dejando a izquierda y derecha sendos intervalos de 15 movimientos.

fig. 7
El disco 4 se mueve en los puntos centrales de cada intervalo de 15, dejando intervalos de 7. Los movimientos del disco 4 están separados por 15 movimientos, el primero a 7 movimientos del principio y el último a 7 movimientos del final.

fig. 8
El disco 3 se mueve en los puntos centrales de cada intervalo de 7, dejando intervalos de 3. Los movimientos del disco 4 están separados por 7 movimientos, el primero a 3 movimientos del principio y el último a 3 movimientos del final.

fig. 9
El disco 2 se mueve en los puntos centrales de cada intervalo de 3, dejando huecos de un solo movimiento. Los movimientos del disco 2 están separados por 3 movimientos, el primero a 1 movimiento del principio y el último a 1 movimiento del final.

fig. 10
Por fin, el disco 1 interviene en todos los movimientos que quedan, incluyendo el primero y el último. Se desplaza por tanto, como ya sabíamos, una vez sí y otra vez no.

fig. 11
En general, el disco k se mueve en 2n−k ocasiones, hay entre cada movimiento y el siguiente 2k−1 movimientos, y su primer y último movimiento están separados 2k−1−1 movimientos del principio y del final respectivamente.
Esta distribución de movimientos tiene una estrecha relación con la de unos y ceros en la secuencia de números binarios. Estos son los primeros 32 números (del 0 al 31, todos los que se pueden escribir con cinco dígitos, o más precisamente con cinco bits) en codificación binaria, ordenados por columnas.
00000 01000 10000 11000 00001 01001 10001 11001 00010 01010 10010 11010 00011 01011 10011 11011 00100 01100 10100 11100 00101 01101 10101 11101 00110 01110 10110 11110 00111 01111 10111 11111tabla 1
En cada paso de un número al siguiente hay exactamente un 0 que se cambia por un 1, y este 1 (marcado en negrita en la lista) es siempre el primero contando por la derecha.
Tanto el primer número (00000 no lo tenemos en cuenta) como el último terminan en 1 y entre un número que termina en 1 y el siguiente hay sólo otro separándolos.
El primer número terminado en 10 es 00010, ocupando el segundo (el 10º, en notación binaria) lugar de la lista. El último es 11110, también segundo, pero contando por el final. Entre un número terminado en 10 y el siguiente hay 3 = 22−1 (100−1 en binario).
El primer número terminado en 100 es 00100, el cuarto (el 100º, en notación binaria) de la lista. El último es 11100, cuarto contando por el final. Entre un número terminado en 100 y el siguiente hay 7 = 23−1 (1000−1 en binario).
Igual que hicimos antes con la tira de cuadros (pero en sentido inverso) podríamos seguir hasta el quinto dígito. En general, en la lista de los primeros 2n−1 números binarios (sin contar el 0) usaremos n dígitos (bits). Para cualquier k entre 1 y n, el primer número terminado en un 1 seguido de k−1 ceros está a 2k−1−1 del principio y el último está a la misma distancia del final; entre cualquier número de esta forma y el siguiente hay una separación de 2k−1. En definitiva, estos unos marcados en negrita en la lista indican qué disco interviene en cada movimiento de la Torre de Hanoi. Un ejemplo, volviendo a la torre de ocho discos. Supongamos que queremos saber qué disco se mueve en el movimiento 136. En binario y usando 8 bits, 136 se escribe 10001000, así que se mueve el disco 4, ya que el primer bit con valor uno contando de derecha a izquierda es el cuarto.
Ya que sabemos qué disco se mueve en cada momento, veamos ahora si podemos determinar hacia dónde. Como ya hicimos antes al hablar del algoritmo de Buneman y Levy, consideraremos que el poste A está a la derecha del poste C, así que si un disco está en C y decimos que se mueve hacia la derecha, irá a para a A. Análogamente, un disco en A que se mueve hacia la izquierda irá a parar a C.
En primer lugar, el disco n realiza un solo movimiento hacia la izquierda, como se aprecia en la figura 2 (porque hemos fijado el poste de destino en C; en caso contrario iría hacia la derecha). El disco n−1 se mueve primero de A a B y después a C, desplazándose en ambos casos hacia la derecha. Se ve en la siguiente animación (disco 7).

fig. 12
En general, si un disco k realiza todos sus movimientos hacia un lado, el disco k−1 tiene que hacerlos en sentido contrario. Se puede decir que los movimientos de k−1 consisten en apartarse para permitir los movimientos de k. En conclusión, cada disco se desplaza siempre en una dirección fija: hacia la izquierda si n−k es par y hacia la derecha si n−k es impar. El movimiento del disco 1 que vimos antes es una consecuencia de esto.
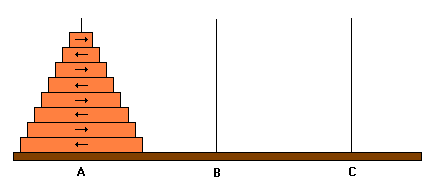
fig. 13
Sabemos ya qué disco se mueve en cada momento y en qué dirección. Siguiendo con el ejemplo de antes, en una torre de 8 discos, el movimiento número 136 (10001000 en binario) lo realiza el disco 4 hacia la izquierda (porque 8−4 es par).
Estamos en condiciones de escribir un tercer algoritmo iterativo basado en los números binarios.
Es posible también determinar directamente a partir de la forma binaria de m el poste de origen y de destino del movimiento (en lugar del disco a mover y la dirección del movimiento), obteniéndose un algoritmo muy corto y rápido. (Este algoritmo aparece en la página de M. Kolar.)
Antes vimos que la representación binaria del número de cada movimiento de la solución nos mostraba qué disco se movía y en qué dirección. Ahora vamos a ver que es posible incluso determinar en qué poste se encuentra cada disco, de acuerdo con el método descubierto por Timothy R. S. Walsh. La idea es ir colocando los discos por orden decreciente de tamaño.
La nueva idea clave es que el disco k se encuentra sobre el disco k+1 si, y sólo si, en la representación binaria del número de movimiento los bits k y k+1 (contando de derecha a izquierda) coinciden. Con esto y el hecho ya conocido de que sólo pueden estar en contacto discos de distinta paridad es posible ir colocando todos los discos. Si suponemos que las bases de los postes están los discos n+1, n+2 y n+3 no hace falta tratar el disco n como una excepción; estará en el poste inicial cuando el bit de la izquierda sea 0 y en el poste de destino cuando sea 1. Para mayor facilidad podemos colorear el puzzle como en la figura 4.
Por ejemplo, después del movimiento 136 (010001000), el disco 8 (010001000) no está sobre el «disco 9», es decir, sobre la base del poste inicial, así que tiene que estar sobre el 11 (la base del poste de destino). El disco 7 (010001000) no se encuentra encima del 8, así que, por paridad, tiene que estar sobre el 10 (base del poste B). El disco 6 (010001000) se encuentra sobre el 7, y el 5 (010001000) sobre el 6. El disco 4 (010001000) no está encima del 5, así que está en el poste A (no puede estar en C, porque tendría que colocarse encima del 8, que tiene la misma paridad). El disco 3 (010001000) no está sobre el 4, y por paridad está sobre el 8, en el poste C (arriba del poste B está 5, impar como 3). Para terminar, el disco 2 (010001000) está encima del 3 y el 1 (010001000) está encima del 2. La siguiente animación ilustra todo el proceso.

fig. 14
Rodolfo Valeiras
Última modificación: 26 de julio de 2004