El skewb ultimate es una variante del skewb con forma de dodecaedro regular. Hay versiones con doce colores, uno por cara, y otras con seis colores, con las caras opuestas del mismo color.

Aunque la forma de dodecaedro pueda confundirnos al principio, el skewb ultimate está íntimamente emparentado con el skewb normal. La estructura interna es la misma y todas las piezas se corresponden, variando en la forma y el coloreado. Las piezas centro del skewb se convierten en el ultimate en piezas con cuatro facetas (dos pentagonales más grandes y dos más pequeñas con forma de rombo) situadas en seis de las 30 aristas del dodecaedro. Las esquinas del skewb se deforman solo un poco para acoplarse a ocho de los 20 vértices. Podemos convertir un ultimate en un skew normal poniéndole pegatinas.

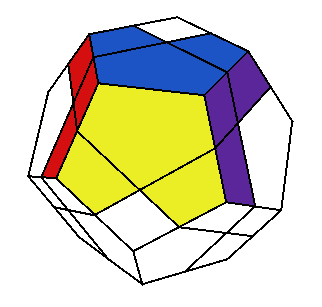
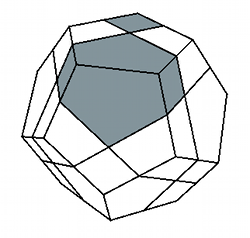
En la imagen anterior, las ocho facetas verdes se corresponden con las cuatro de una cara del skewb. También podemos hacer que un skewb sea equivalente a un skewb ultimate haciendo visible la orientación de los centros, por ejemplo poniendo una marca de color en cada esquina.

Esta variante del skewb fue comercializada inicialmente por Uwe Meffert con el nombre de Pyraminx Ball. Posiblemente el propio Meffert fuera su inventor original, aunque Tony Fisher tuvo la misma idea posteriormente.
El skewb ultimate añade a los estados posibles del skewb los derivados de la orientación de los centros. Esto supone 32 veces más estados: 100.776.960. Mediante un análisis computerizado exhaustivo se ha comprobado que todas las posiciones se pueden resolver en 14 o menos movimientos (véase 2).
La estructura interna es la misma que la del skewb normal, tan solo las piezas tienen otro diseño para adoptar la forma de dodecaedro.


Hay dos clases de piezas. que llamaremos piezas borde y piezas esquina. Hay seis piezas borde, con cuatro facetas; y ocho piezas esquina, con tres facetas. Cuatro de las piezas esquina están sueltas y las otras cuatro están en los extremos del «esqueleto interno». En la versión de doce colores, no hay dos piezas con los mismos colores. En la versión de seis colores, todas las piezas tienen una versión «reflejada», con los mismos colores pero en otro orden.
El skewb ultimate es solo un poco más difícil que el skewb original. Meffert le asigna dificultad 3 (entre 1 y 6).
Podemos manejar el skewb ultimate imaginando que es un skewb normal, como si sus piezas esquina fueran las esquinas del skewb y sus piezas borde los centros del skewb. La colocación y los movimientos del skewb ultimate serán también los del correspondiente skewb inscrito, como se ve en el siguiente dibujo (los vértices G —debajo de F— y H —debajo de E— están ocultos).
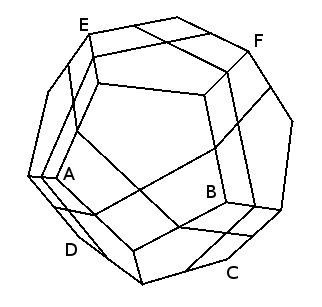
Con respecto al dibujo anterior (y los que vienen a continuación) hay que tener en cuenta dos cosas: primero, que el dodecaedro está un poco inclinado hacia el frente, de forma que la pieza borde de arriba se representa en realidad entre arriba y al frente; y segundo, que es posible que esta pieza esté en la otra posición, con la arista larga que separa los dos pentágonos en dirección perpendicular a la que tiene en la imagen.
Los movimientos en sentido horario se representarán mediante la letra del vértice en minúsculas, y el inverso con -1 como superíndice.
Los movimientos del dodecaedro como un todo los representaremos mediante las letras X, Y, Z correspondientes a los ejes cartesianos. X es perpendicular al plano de los vértices B, F, G y C; Y es perpendicular al plano de los vértices A, B, F y E; y Z es perpendicular al plano de los vértices A, B, C y D. Un giro X es un giro de un cuarto de vuelta en torno al eje X en sentido horario y un giro X-1 lo mismo, pero antihorario.
Los movimientos de vértices opuestos, por ejemplo C y E, se pueden considerar equivalentes. El movimiento c tiene el mismo efecto que el movimiento e salvo en la orientación global del puzzle. Así que podríamos usar solo giros de cuatro de los ocho vértices, por ejemplo A, B, C y D, o, como hace Jaap Scherphuis, A, C, F y H (aunque su notación es diferente).
El siguiente método de resolución equivale al del skewb normal con una fase final para orientar los bordes. Es un método sencillo, que usa casi exclusivamente dos movimientos simples, a y b (y sus inversos), pero no está optimizado en cuanto a su longitud. Para soluciones más cortas, consultar las páginas de Jaap Scherphuis (2).
El método vale para ambas versiones de 6 y 12 colores. La versión de 6 colores resulta un poco más confusa porque hay que fijarse mejor para diferenciar las piezas, pero no supone un cambio de dificultad apreciable.
Elegimos una pieza borde cualquiera y ponemos a su lado las cuatro piezas esquina vecinas. Esta fase es lo suficientemente intuitiva como para que no merezca la pena detallarla (en la página del skewb sí se explica con detalle la fase análoga).
Una vez colocadas las cuatro primeras piezas esquina, las otras cuatro también estarán en sus posiciones correctas, normalmente no bien orientadas. Le damos la vuelta al puzzle y lo ponemos de forma que la pieza borde superior tenga una de las facetas grandes de nuestro lado. Identificamos el color que se repite en las dos piezas esquina adyacentes; ese es el color que debe estar arriba (no hay que dejarse confundir por el color de la pieza borde, que seguramente no coincidirá). Podemos reducir las posibilidades a las siguientes cinco:

Cada pieza esquina lleva una de las etiquetas 0, + o —. Si está bien orientada lleva un 0; si está girada en sentido horario lleva un +; si está girada en sentido antihorario lleva un —. No hace falta mirar las piezas de atrás, porque la orientación de las cuatro esquinas está ligada de forma que conociendo las del frente deducimos las de las otras dos. Si la configuración no se corresponde con ninguna de estas basta girar el puzzle 180 grados (Y2; el color será distinto, claro).
Recordemos que la secuencia ab-1a-1b gira en sentido horario las dos esquinas frontales y en sentido antihorario las dos traseras (sin tocar las piezas de abajo ya colocadas). Teniendo esto en cuenta, repasemos los casos de izquierda a derecha:
La pieza borde de abajo está bien colocada y orientada; las demás normalmente no lo estarán. Para saber si una pieza está bien colocada nos fijamos en las piezas esquina adyacentes, teniendo en cuenta que la pieza borde puede estar volteada, con los colores al revés.
Si la pieza de arriba no está bien colocada, orientamos el puzzle de forma que tengamos al frente el borde donde debe ir y ejecutamos (ab-1a-1b Y2)2. Después de esto habrá tres o cuatro piezas borde mal colocadas (o ninguna).
Si las tres piezas mal colocadas están alineadas, ponemos el puzzle de forma que la pieza de arriba deba ir al frente (como indican las flechas del primer dibujo) y ejecutamos (ab-1a-1b Y2)2. Si están formando un triángulo, hay que hacer antes y después un movimiento de ajuste. Ponemos el puzzle de forma que las piezas a colocar estén arriba, al frente y a la derecha. Si el ciclo sigue el sentido de las agujas del reloj, el movimiento f nos pone en la situación anterior, así que la secuencia completa es f (ab-1a-1b Y2)2 f. Si el ciclo es en sentido contrario, después de f hay que girar el dodecaedro: f (Y2 ab-1a-1b)2 f.
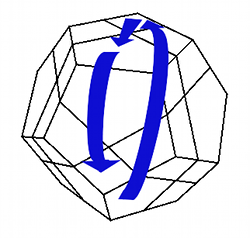

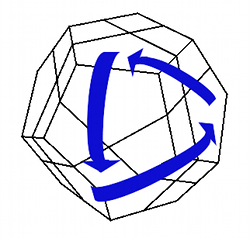
Si hay cuatro piezas borde mal colocadas tienen que estar intercambiadas a pares (no puede haber un 4-ciclo). Hay dos casos posibles: que las cuatro piezas estén alineadas formando un anillo alrededor del dodecaedro, o que no. En el primer caso colocamos el puzzle con el anillo en la dirección frente-atrás (dirección Z) y ejecutamos ab-1a-1b. Esto reducirá el número de piezas borde mal colocadas a 3.
En el otro caso podemos colocar el puzzle de una de las siguientes formas:


El primer caso se resuelve con (ab-1a-1b)3, el segundo con (b-1a-1ba)3, y el tercero con (aba-1b-1)3.
Esta es la única fase novedosa con respecto al skewb normal. Después de colocar todas las piezas borde puede haber varias de ellas volteadas. En concreto pueden ser 2 o 4 piezas, porque tiene que ser un número par y no pueden ser 6 porque hay una que está bien desde el principio. Para orientarlas correctamente vamos a usar dos secuencias: (ab-1a-1b)6, que afecta a cuatro piezas, arriba, frente, izquierda y derecha (imagen izquierda); y ab-1a-1b Y2 (ab-1a-1b)2 Y2 ab-1a-1b, que afecta a dos piezas, arriba y atrás (imagen derecha).

Si las dos piezas son contiguas se orienta el puzzle de forma que estén arriba y atrás y se ejecuta la segunda secuencia.
Si son opuestas, hacemos que estén al frente y atrás y ejecutamos b <segunda secuencia> b-1. Los dos últimos movimientos son b y b-1, que se anulan.
Si las cuatro piezas no forman un anillo (las piezas borde bien orientadas son contiguas) los colocamos de forma que las piezas a voltear estén a la izquierda, a la derecha, arriba y al frente (primera imagen) y ejecutamos la primera secuencia, (ab-1a-1b)6. Alternativamente, podemos ejecutar la secuencia (adaptada de 2) a-1c-1ab-1c-1 a-1cac-1 bac, con 12 movimientos menos.
Si las cuatro piezas forman un anillo (las piezas bien orientadas están en posiciones opuestas) lo podemos reducir al caso anterior poniendo al frente una de las piezas bien orientadas y ejecutando d (ab-1a-1b)6 d-1. Alternativamente, podemos ahorrarnos de nuevo 12 movimientos con d a-1c-1ab-1c-1 a-1cac-1 bac d-1.
Rodolfo Valeiras Reina, 11 de mayo de 2013.